Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
Bernoulli numbers are a sequence of rational numbers useful for the Taylor series expansion, Euler-Maclaurin formula, and the Riemann zeta function.
Bernoulli numbers are used in evaluation of some Boost.Math functions, including the tgamma, lgamma and polygamma functions.
#include <boost/math/special_functions/bernoulli.hpp>
namespace boost { namespace math { template <class T> T bernoulli_b2n(const int n); // Single Bernoulli number (default policy). template <class T, class Policy> T bernoulli_b2n(const int n, const Policy &pol); // User policy for errors etc. }} // namespaces
Both return the (2 * n)th Bernoulli number B2n.
Note that since all odd numbered Bernoulli numbers are zero (apart from B1 which is -½) the interface will only return the even numbered Bernoulli numbers.
This function uses fast table lookup for low-indexed Bernoulli numbers, while
larger values are calculated as needed and then cached. The caching mechanism
requires a certain amount of thread safety code, so unchecked_bernoulli_b2n
may provide a better interface for performance critical code.
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use, etc.
Refer to Policies for more details.
A simple example computes the value of B4 where the return type is double, note that the argument to bernoulli_b2n
is 2 not 4 since it computes B2N.
try { // It is always wise to use try'n'catch blocks around Boost.Math functions // so that any informative error messages can be displayed in the catch block. std::cout << std::setprecision(std::numeric_limits<double>::digits10) << boost::math::bernoulli_b2n<double>(2) << std::endl;
So B4 == -1/30 == -0.0333333333333333
If we use Boost.Multiprecision and its 50 decimal digit floating-point type
cpp_dec_float_50, we can
calculate the value of much larger numbers like B200
and also obtain much
higher precision.
std::cout << std::setprecision(std::numeric_limits<boost::multiprecision::cpp_dec_float_50>::digits10) << boost::math::bernoulli_b2n<boost::multiprecision::cpp_dec_float_50>(100) << std::endl;
-3.6470772645191354362138308865549944904868234686191e+215
#include <boost/math/special_functions/bernoulli.hpp>
template <> struct max_bernoulli_b2n<T>; template<class T> inline T unchecked_bernoulli_b2n(unsigned n);
unchecked_bernoulli_b2n provides
access to Bernoulli numbers without any checks for
overflow or invalid parameters. It is implemented as a direct
(and very fast) table lookup, and while not recomended for general use it
can be useful inside inner loops where the ultimate performance is required,
and error checking is moved outside the loop.
The largest value you can pass to unchecked_bernoulli_b2n<> is max_bernoulli_b2n<>::value:
passing values greater than that will result in a buffer overrun error, so
it's clearly important to place the error handling in your own code when
using this direct interface.
The value of boost::math::max_bernoulli_b2n<T>::value varies by the type T, for types
float/double/long double
it's the largest value which doesn't overflow the target type: for example,
boost::math::max_bernoulli_b2n<double>::value is 129. However, for multiprecision
types, it's the largest value for which the result can be represented as
the ratio of two 64-bit integers, for example boost::math::max_bernoulli_b2n<boost::multiprecision::cpp_dec_float_50>::value
is just 17. Of course larger indexes can be passed to bernoulli_b2n<T>(n), but
then then you loose fast table lookup (i.e. values may need to be calculated).
/*For example: */ std::cout << "boost::math::max_bernoulli_b2n<float>::value = " << boost::math::max_bernoulli_b2n<float>::value << std::endl; std::cout << "Maximum Bernoulli number using float is " << boost::math::bernoulli_b2n<float>( boost::math::max_bernoulli_b2n<float>::value) << std::endl; std::cout << "boost::math::max_bernoulli_b2n<double>::value = " << boost::math::max_bernoulli_b2n<double>::value << std::endl; std::cout << "Maximum Bernoulli number using double is " << boost::math::bernoulli_b2n<double>( boost::math::max_bernoulli_b2n<double>::value) << std::endl;
boost::math::max_bernoulli_b2n<float>::value = 32 Maximum Bernoulli number using float is -2.0938e+038 boost::math::max_bernoulli_b2n<double>::value = 129 Maximum Bernoulli number using double is 1.33528e+306
#include <boost/math/special_functions/bernoulli.hpp>
namespace boost { namespace math { // Multiple Bernoulli numbers (default policy). template <class T, class OutputIterator> OutputIterator bernoulli_b2n( int start_index, unsigned number_of_bernoullis_b2n, OutputIterator out_it); // Multiple Bernoulli numbers (user policy). template <class T, class OutputIterator, class Policy> OutputIterator bernoulli_b2n( int start_index, unsigned number_of_bernoullis_b2n, OutputIterator out_it, const Policy& pol); }} // namespaces
Two versions of the Bernoulli number function are provided to compute multiple Bernoulli numbers with one call (one with default policy and the other allowing a user-defined policy).
These return a series of Bernoulli numbers:
B2*start_index,B2*(start_index+1),...,B2*(start_index+number_of_bernoullis_b2n-1)
We can compute and save all the float-precision Bernoulli numbers from one call.
std::vector<float> bn; // Space for 32-bit `float` precision Bernoulli numbers. // Start with Bernoulli number 0. boost::math::bernoulli_b2n<float>(0, 32, std::back_inserter(bn)); // Fill vector with even Bernoulli numbers. for(size_t i = 0; i < bn.size(); i++) { // Show vector of even Bernoulli numbers, showing all significant decimal digits. std::cout << std::setprecision(std::numeric_limits<float>::digits10) << i*2 << ' ' << bn[i] << std::endl; }
0 1 2 0.166667 4 -0.0333333 6 0.0238095 8 -0.0333333 10 0.0757576 12 -0.253114 14 1.16667 16 -7.09216 18 54.9712 20 -529.124 22 6192.12 24 -86580.3 26 1.42552e+006 28 -2.72982e+007 30 6.01581e+008 32 -1.51163e+010 34 4.29615e+011 36 -1.37117e+013 38 4.88332e+014 40 -1.92966e+016 42 8.41693e+017 44 -4.03381e+019 46 2.11507e+021 48 -1.20866e+023 50 7.50087e+024 52 -5.03878e+026 54 3.65288e+028 56 -2.84988e+030 58 2.38654e+032 60 -2.14e+034 62 2.0501e+036
Of course, for any floating-point type, there is a maximum Bernoulli number that can be computed before it overflows the exponent. By default policy, if we try to compute too high a Bernoulli number, an exception will be thrown.
try { std::cout << std::setprecision(std::numeric_limits<float>::digits10) << "Bernoulli number " << 33 * 2 <<std::endl; std::cout << boost::math::bernoulli_b2n<float>(33) << std::endl; } catch (std::exception ex) { std::cout << "Thrown Exception caught: " << ex.what() << std::endl; }
and we will get a helpful error message (provided try'n'catch blocks are used).
Bernoulli number 66 Thrown Exception caught: Error in function boost::math::bernoulli_b2n<float>(n): Overflow evaluating function at 33
The source of this example is at bernoulli_example.cpp
All the functions usually return values within one ULP (unit in the last place) for the floating-point type.
The implementation details are in bernoulli_details.hpp and unchecked_bernoulli.hpp.
For i <=
max_bernoulli_index<T>::value this is implemented by simple table
lookup from a statically initialized table; for larger values of i, this is implemented by the Tangent Numbers
algorithm as described in the paper: Fast Computation of Bernoulli, Tangent
and Secant Numbers, Richard P. Brent and David Harvey, http://arxiv.org/pdf/1108.0286v3.pdf
(2011).
Tangent (or Zag) numbers (an even alternating permutation number) are defined and their generating function is also given therein.
The relation of Tangent numbers with Bernoulli numbers Bi is given by Brent and Harvey's equation 14:

Their relation with Bernoulli numbers Bi are defined by
if i > 0 and i is even then 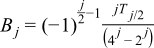
elseif
i == 0 then Bi = 1
elseif i == 1 then Bi
= -1/2
elseif i < 0 or i is odd then Bi =
0
Note that computed values are stored in a fixed-size table, access is thread safe via atomic operations (i.e. lock free programming), this imparts a much lower overhead on access to cached values than might overwise be expected - typically for multiprecision types the cost of thread synchronisation is negligable, while for built in types this code is not normally executed anyway. For very large arguments which cannot be reasonably computed or stored in our cache, an asymptotic expansion due to Luschny is used: