 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/distributions/exponential.hpp>
template <class RealType = double, class Policy = policies::policy<> > class exponential_distribution; typedef exponential_distribution<> exponential; template <class RealType, class Policy> class exponential_distribution { public: typedef RealType value_type; typedef Policy policy_type; exponential_distribution(RealType lambda = 1); RealType lambda()const; };
The exponential distribution is a continuous probability distribution with PDF:
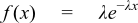
It is often used to model the time between independent events that happen at a constant average rate.
The following graph shows how the distribution changes for different values of the rate parameter lambda:

exponential_distribution(RealType lambda = 1);
Constructs an Exponential distribution with parameter lambda. Lambda is defined as the reciprocal of the scale parameter.
Requires lambda > 0, otherwise calls domain_error.
RealType lambda()const;
Accessor function returns the lambda parameter of the distribution.
All the usual non-member accessor functions that are generic to all distributions are supported: Cumulative Distribution Function, Probability Density Function, Quantile, Hazard Function, Cumulative Hazard Function, mean, median, mode, variance, standard deviation, skewness, kurtosis, kurtosis_excess, range and support.
The domain of the random variable is [0, +∞].
The exponential distribution is implemented in terms of the standard library
functions exp, log, log1p
and expm1 and as such should
have very low error rates.
In the following table λ is the parameter lambda of the distribution, x is the random variate, p is the probability and q = 1-p.
|
Function |
Implementation Notes |
|---|---|
|
|
Using the relation: pdf = λ * exp(-λ * x) |
|
cdf |
Using the relation: p = 1 - exp(-x * λ) = -expm1(-x * λ) |
|
cdf complement |
Using the relation: q = exp(-x * λ) |
|
quantile |
Using the relation: x = -log(1-p) / λ = -log1p(-p) / λ |
|
quantile from the complement |
Using the relation: x = -log(q) / λ |
|
mean |
1/λ |
|
standard deviation |
1/λ |
|
mode |
0 |
|
skewness |
2 |
|
kurtosis |
9 |
|
kurtosis excess |
6 |
(See also the reference documentation for the related Extreme Distributions.)