 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/special_functions/hermite.hpp>
namespace boost{ namespace math{ template <class T> calculated-result-type hermite(unsigned n, T x); template <class T, class Policy> calculated-result-type hermite(unsigned n, T x, const Policy&); template <class T1, class T2, class T3> calculated-result-type hermite_next(unsigned n, T1 x, T2 Hn, T3 Hnm1); }} // namespaces
The return type of these functions is computed using the result
type calculation rules: note than when there is a single
template argument the result is the same type as that argument or double if the template argument is an integer
type.
template <class T> calculated-result-type hermite(unsigned n, T x); template <class T, class Policy> calculated-result-type hermite(unsigned n, T x, const Policy&);
Returns the value of the Hermite Polynomial of order n at point x:
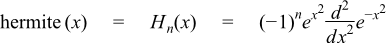
The final Policy argument is optional and can be used to control the behaviour of the function: how it handles errors, what level of precision to use etc. Refer to the policy documentation for more details.
The following graph illustrates the behaviour of the first few Hermite Polynomials:

template <class T1, class T2, class T3> calculated-result-type hermite_next(unsigned n, T1 x, T2 Hn, T3 Hnm1);
Implements the three term recurrence relation for the Hermite polynomials, this function can be used to create a sequence of values evaluated at the same x, and for rising n.

For example we could produce a vector of the first 10 polynomial values using:
double x = 0.5; // Abscissa value vector<double> v; v.push_back(hermite(0, x)).push_back(hermite(1, x)); for(unsigned l = 1; l < 10; ++l) v.push_back(hermite_next(l, x, v[l], v[l-1]));
Formally the arguments are:
The degree n of the last polynomial calculated.
The abscissa value
The value of the polynomial evaluated at degree n.
The value of the polynomial evaluated at degree n-1.
The following table shows peak errors (in units of epsilon) for various domains of input arguments. Note that only results for the widest floating point type on the system are given as narrower types have effectively zero error.
Table 3.19. Peak Errors In the Hermite Polynomial
|
Significand Size |
Platform and Compiler |
Errors in range 0 < l < 20 |
|---|---|---|
|
53 |
Win32, Visual C++ 8 |
Peak=4.5 Mean=1.5 |
|
64 |
Red Hat Linux IA32, g++ 4.1 |
Peak=6 Mean=2 |
|
64 |
Red Hat Linux IA64, g++ 3.4.4 |
Peak=6 Mean=2 |
|
113 |
HPUX IA64, aCC A.06.06 |
Peak=6 Mean=4 |
Note that the worst errors occur when the degree increases, values greater than ~120 are very unlikely to produce sensible results, especially in the associated polynomial case when the order is also large. Further the relative errors are likely to grow arbitrarily large when the function is very close to a root.
A mixture of spot tests of values calculated using functions.wolfram.com, and randomly generated test data are used: the test data was computed using NTL::RR at 1000-bit precision.
These functions are implemented using the stable three term recurrence relations. These relations guarentee low absolute error but cannot guarentee low relative error near one of the roots of the polynomials.