 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
Bessel Functions are solutions to Bessel's ordinary differential equation:

where ν is the order of the equation, and may be an arbitrary real or complex number, although integer orders are the most common occurrence.
This library supports either integer or real orders.
Since this is a second order differential equation, there must be two linearly independent solutions, the first of these is denoted Jv and known as a Bessel function of the first kind:

This function is implemented in this library as cyl_bessel_j.
The second solution is denoted either Yv or Nv and is known as either a Bessel Function of the second kind, or as a Neumann function:

This function is implemented in this library as cyl_neumann.
The Bessel functions satisfy the recurrence relations:


Have the derivatives:


Have the Wronskian relation:

and the reflection formulae:


The Bessel functions are valid for complex argument x, and an important special case is the situation where x is purely imaginary: giving a real valued result. In this case the functions are the two linearly independent solutions to the modified Bessel equation:

The solutions are known as the modified Bessel functions of the first and second kind (or occasionally as the hyperbolic Bessel functions of the first and second kind). They are denoted Iv and Kv respectively:


These functions are implemented in this library as cyl_bessel_i and cyl_bessel_k respectively.
The modified Bessel functions satisfy the recurrence relations:


Have the derivatives:

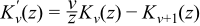
Have the Wronskian relation:

and the reflection formulae:


When solving the Helmholtz equation in spherical coordinates by separation of variables, the radial equation has the form:

The two linearly independent solutions to this equation are called the spherical Bessel functions jn and yn , and are related to the ordinary Bessel functions Jn and Yn by:

The spherical Bessel function of the second kind yn is also known as the spherical Neumann function nn.
These functions are implemented in this library as sph_bessel and sph_neumann.