 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
The Boost.Geometry.Index is intended to gather data structures called spatial indexes which may be used to accelerate searching for objects in space. In general, spatial indexes stores geometric objects' representations and allows searching for objects occupying some space or close to some point in space.
Currently, only one spatial index is implemented - R-tree.
R-tree is a tree data structure used for spatial searching. It was proposed by Antonin Guttman in 1984 [1] as an expansion of B-tree for multi-dimensional data. It may be used to store points or volumetric data in order to perform a spatial query. This query may for example return objects that are inside some area or are close to some point in space [2]. It's possible to insert new objects or to remove the ones already stored.
The R-tree structure is presented on the image below. Each R-tree's node store a box describing the space occupied by its children nodes. At the bottom of the structure, there are leaf-nodes which contains values (geometric objects representations).
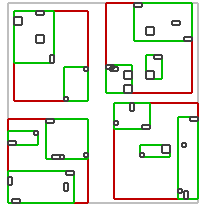
The R-tree is a self-balanced data structure. The key part of balancing algorithm is node splitting algorithm [3] [4]. Each algorithm produces different splits so the internal structure of a tree may be different for each one of them. In general, more complex algorithms analyses elements better and produces less overlapping nodes. In the searching process less nodes must be traversed in order to find desired objects. On the other hand more complex analysis takes more time. In general faster inserting will result in slower searching and vice versa. The performance of the R-tree depends on balancing algorithm, parameters and data inserted into the container.
Additionally there are also algorithms creating R-tree containing some, number of objects. This technique is called bulk loading and is done by use of packing algorithm [5] [6]. This method is faster and results in R-trees with better internal structure. This means that the query performance is increased.
The examples of structures of trees created by use of different algorithms and exemplary operations times are presented below.
|
Linear algorithm |
Quadratic algorithm |
R*-tree |
Packing algorithm |
|
|---|---|---|---|---|
|
Example structure |
|
|
|
|
|
1M Values inserts |
1.76s |
2.47s |
6.19s |
0.64s |
|
100k spatial queries |
2.21s |
0.51s |
0.12s |
0.07s |
|
100k knn queries |
6.37s |
2.09s |
0.64s |
0.52s |
The configuration of the machine used for testing was: Intel(R)
Core(TM) i7 870 @ 2.93GHz, 8GB RAM, MS Windows 7 x64. The code
was compiled with optimization for speed (O2).
The performance of the R-tree for different values of Max parameter and Min=0.5*Max is presented in the table below. In the two upper figures you can see the performance of the R-tree storing random, relatively small, non-overlapping, 2d boxes. In the lower ones, the performance of the R-tree also storing random, 2d boxes, but this time quite big and possibly overlapping. As you can see, the R-tree performance is different in both cases.
|
building |
querying |
|
|---|---|---|
|
non overlapping |
|
|
|
overlapping |
|
|
Key features of this implementation of the R-tree are:
R-tree depends on Boost.Container, Boost.Core, Boost.Move, Boost.MPL, Boost.Range, Boost.Tuple.
The spatial index was originally started by Federico J. Fernandez during the Google Summer of Code 2008 program, mentored by Hartmut Kaiser.
I'd like to thank Barend Gehrels, Bruno Lalande, Mateusz Łoskot, Lucanus J. Simonson for their support and ideas.
[1] Guttman, A. (1984). R-Trees: A Dynamic Index Structure for Spatial Searching
[2] Cheung, K.; Fu, A. (1998). Enhanced Nearest Neighbour Search on the R-tree
[3] Greene, D. (1989). An implementation and performance analysis of spatial data access methods
[4] Beckmann, N.; Kriegel, H. P.; Schneider, R.; Seeger, B. (1990). The R*-tree: an efficient and robust access method for points and rectangles
[5] Leutenegger, Scott T.; Edgington, Jeffrey M.; Lopez, Mario A. (1997). STR: A Simple and Efficient Algorithm for R-Tree Packing
[6] Garcia, Yvan J.; Lopez, Mario A.; Leutenegger, Scott T. (1997). A Greedy Algorithm for Bulk Loading R-trees