 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
 Boost
C++ Libraries
Boost
C++ Libraries
...one of the most highly
regarded and expertly designed C++ library projects in the
world.
— Herb Sutter and Andrei
Alexandrescu, C++
Coding Standards
#include <boost/math/distributions/chi_squared.hpp>
namespace boost{ namespace math{ template <class RealType = double, class Policy = policies::policy<> > class chi_squared_distribution; typedef chi_squared_distribution<> chi_squared; template <class RealType, class Policy> class chi_squared_distribution { public: typedef RealType value_type; typedef Policy policy_type; // Constructor: chi_squared_distribution(RealType i); // Accessor to parameter: RealType degrees_of_freedom()const; // Parameter estimation: static RealType find_degrees_of_freedom( RealType difference_from_mean, RealType alpha, RealType beta, RealType sd, RealType hint = 100); }; }} // namespaces
The Chi-Squared distribution is one of the most widely used distributions in statistical tests. If χi are ν independent, normally distributed random variables with means μi and variances σi2, then the random variable:
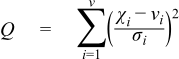
is distributed according to the Chi-Squared distribution.
The Chi-Squared distribution is a special case of the gamma distribution and has a single parameter ν that specifies the number of degrees of freedom. The following graph illustrates how the distribution changes for different values of ν:

chi_squared_distribution(RealType v);
Constructs a Chi-Squared distribution with v degrees of freedom.
Requires v > 0, otherwise calls domain_error.
RealType degrees_of_freedom()const;
Returns the parameter v from which this object was constructed.
static RealType find_degrees_of_freedom( RealType difference_from_variance, RealType alpha, RealType beta, RealType variance, RealType hint = 100);
Estimates the sample size required to detect a difference from a nominal variance in a Chi-Squared test for equal standard deviations.
The difference from the assumed nominal variance that is to be detected: Note that the sign of this value is critical, see below.
The maximum acceptable risk of rejecting the null hypothesis when it is in fact true.
The maximum acceptable risk of falsely failing to reject the null hypothesis.
The nominal variance being tested against.
An optional hint on where to start looking for a result: the current sample size would be a good choice.
Note that this calculation works with variances and not standard deviations.
The sign of the parameter difference_from_variance
is important: the Chi Squared distribution is asymmetric, and the caller
must decide in advance whether they are testing for a variance greater
than a nominal value (positive difference_from_variance)
or testing for a variance less than a nominal value (negative difference_from_variance).
If the latter, then obviously it is a requirement that variance +
difference_from_variance >
0, since no sample can have a negative
variance!
This procedure uses the method in Diamond, W. J. (1989). Practical Experiment Designs, Van-Nostrand Reinhold, New York.
See also section on Sample sizes required in the NIST Engineering Statistics Handbook, Section 7.2.3.2.
All the usual non-member accessor functions that are generic to all distributions are supported: Cumulative Distribution Function, Probability Density Function, Quantile, Hazard Function, Cumulative Hazard Function, mean, median, mode, variance, standard deviation, skewness, kurtosis, kurtosis_excess, range and support.
(We have followed the usual restriction of the mode to degrees of freedom >= 2, but note that the maximum of the pdf is actually zero for degrees of freedom from 2 down to 0, and provide an extended definition that would avoid a discontinuity in the mode as alternative code in a comment).
The domain of the random variable is [0, +∞].
Various worked examples are available illustrating the use of the Chi Squared Distribution.
The Chi-Squared distribution is implemented in terms of the incomplete gamma functions: please refer to the accuracy data for those functions.
In the following table v is the number of degrees of freedom of the distribution, x is the random variate, p is the probability, and q = 1-p.
|
Function |
Implementation Notes |
|---|---|
|
|
Using the relation: pdf = gamma_p_derivative(v / 2, x / 2) / 2 |
|
cdf |
Using the relation: p = gamma_p(v / 2, x / 2) |
|
cdf complement |
Using the relation: q = gamma_q(v / 2, x / 2) |
|
quantile |
Using the relation: x = 2 * gamma_p_inv(v / 2, p) |
|
quantile from the complement |
Using the relation: x = 2 * gamma_q_inv(v / 2, p) |
|
mean |
v |
|
variance |
2v |
|
mode |
v - 2 (if v >= 2) |
|
skewness |
2 * sqrt(2 / v) == sqrt(8 / v) |
|
kurtosis |
3 + 12 / v |
|
kurtosis excess |
12 / v |